Learning Objective

• Calculate the concentration of a diluted solution.

A serial dilution is the stepwise dilution of a substance in solution. Usually the dilution factor at each step is constant, resulting in a geometric progression of the concentration in a logarithmic fashion. A ten-fold serial dilution could be 1 M, 0.1 M, 0.01 M, 0.001 M.

1. Serial dilution Definition. Serial dilution, as the name suggests, is a series of sequential dilutions that are performed to convert a dense solution into a more usable concentration. In simple words, serial dilution is the process of stepwise dilution of a solution with an associated dilution factor.
2. When do I use the serial dilution technique instead of the parallel dilution technique? Another way to make dilutions is to use some of your existing stock solution to make a dilute solution, then use some of the dilute solution to make an even more dilute solution, then use some of that solution to make an even more dilute solution, and so on.
3. Sep 16, 2019 Serial Vs Parallel Dilution Parallel dilution is the dilution of a solution with equalquantity of the same solvent with which the solution is made. E.g.,1mL of 100µg/ml strength aqueous solution can be diluted to 2mL of50µg/mL strength solution by adding 1mL Water.

Key Points

• Most commonly, a solution’s concentration is expressed in terms of mass percent, mole fraction, molarity, molality, and normality. When calculating dilution factors, it is important that the units of volume and concentration remain consistent.
• Dilution calculations can be performed using the formula M₁V₁ = M₂V₂.
• A serial dilution is a series of stepwise dilutions, where the dilution factor is held constant at each step.

Terms

• dilutiona solution that has had additional solvent, such as water, added to make it less concentrated
• serial dilutionstepwise dilution of a substance in solution

Dilution refers to the process of adding additional solvent to a solution to decrease its concentration. This process keeps the amount of solute constant, but increases the total amount of solution, thereby decreasing its final concentration. Dilution can also be achieved by mixing a solution of higher concentration with an identical solution of lesser concentration. Diluting solutions is a necessary process in the laboratory, as stock solutions are often purchased and stored in very concentrated forms. For the solutions to be usable in the lab (for a titration, for instance), they must be accurately diluted to a known, lesser concentration.

The volume of solvent needed to prepare the desired concentration of a new, diluted solution can be calculated mathematically. The relationship is as follows:

[latex]M_1V_1=M_2V_2[/latex]

M₁ denotes the concentration of the original solution, and V1 denotes the volume of the original solution; M₂ represents the concentration of the diluted solution, and V2 represents the final volume of the diluted solution. When calculating dilution factors, it is important that the units for both volume and concentration are the same for both sides of the equation.

Example

• 175 mL of a 1.6 M aqueous solution of LiCl is diluted with water to a final volume of 1.0 L. What is the final concentration of the diluted solution?
• [latex]M_1V_1=M_2V_2[/latex]
• (1.6 M)(175 mL) = M₂(1000 mL)
• M₂ = 0.28 M

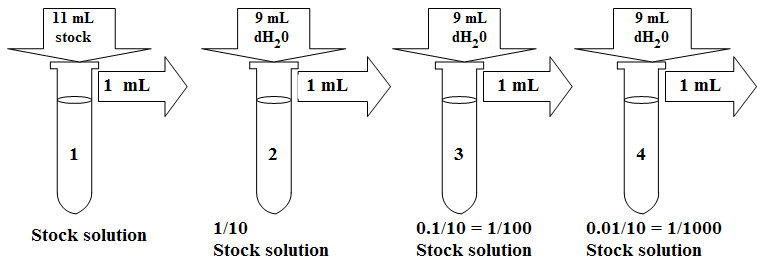
Serial Dilutions

Serial dilutions involve diluting a stock or standard solution multiple times in a row. Typically, the dilution factor remains constant for each dilution, resulting in an exponential decrease in concentration. For example, a ten-fold serial dilution could result in the following concentrations: 1 M, 0.1 M, 0.01 M, 0.001 M, and so on. As is evidenced in this example, the concentration is reduced by a factor of ten in each step. Serial dilutions are used to accurately create extremely diluted solutions, as well as solutions for experiments that require a concentration curve with an exponential or logarithmic scale. Serial dilutions are widely used in experimental sciences, including biochemistry, pharmacology, microbiology, and physics.

Show Sources

Boundless vets and curates high-quality, openly licensed content from around the Internet. This particular resource used the following sources:

http://www.boundless.com/
Boundless Learning
CC BY-SA 3.0.

http://en.wikipedia.org/wiki/serial%20dilution
Wikipedia
CC BY-SA 3.0.

http://en.wiktionary.org/wiki/dilution
Wiktionary
CC BY-SA 3.0.

http://en.wikipedia.org/wiki/Serial_dilution
Wikipedia
CC BY-SA 3.0.

http://cnx.org/content/m17123/latest/
OpenStax CNX
CC BY 3.0.

http://commons.wikimedia.org/wiki/File:Dilution-concentration_simple_example.jpg
Wikimedia
CC BY-SA.

This section is not a recipe for your experiment. It explains someprinciples for designing dilutions that give optimal results. Onceyou understand these principles, you will be better able to designthe dilutions you need for each specific case.

Often in experimental work, you need to cover a range ofconcentrations, so you need to make a bunch of differentdilutions. For example, you need to do such dilutions of thestandard IgG to make the standard curve in ELISA, and then againfor the unknown samples in ELISA.

You might think it would be good to dilute 1/2, 1/3, 1/10, 1/100.These seem like nice numbers. There are two problems with this series ofdilutions.

Serial Dilution Vs Parallel Dilution

1. The dilutions are unnecessarily complicated to make. You need to do a differentcalculation, and measure different volumes, for each one. It takes a longtime, and it is too easy to make a mistake.
2. The dilutions cover the range from 1/2 to 1/100 unevenly.In fact, the 1/2 vs. 1/3 dilutions differ by only 1.5-fold in concentration,while the 1/10 vs. 1/100 dilutions differ by ten-fold. If you are going tomeasure results for four dilutions, it is a waste of time and materialsto make two of them almost the same. And what if the half-maximal signaloccurs between 1/10 and 1/100? You won't be able to tell exactly where itis because of the big space between those two.

Serial dilutions are much easier to make and they cover the range evenly.

Serial dilutions are made by making the same dilution step over and over,using the previous dilution as the input to the next dilution in each step.Since the dilution-fold is the same in each step, the dilutionsare a geometric series (constant ratio between any adjacent dilutions).For example:

1/3, 1/9, 1/27, 1/81

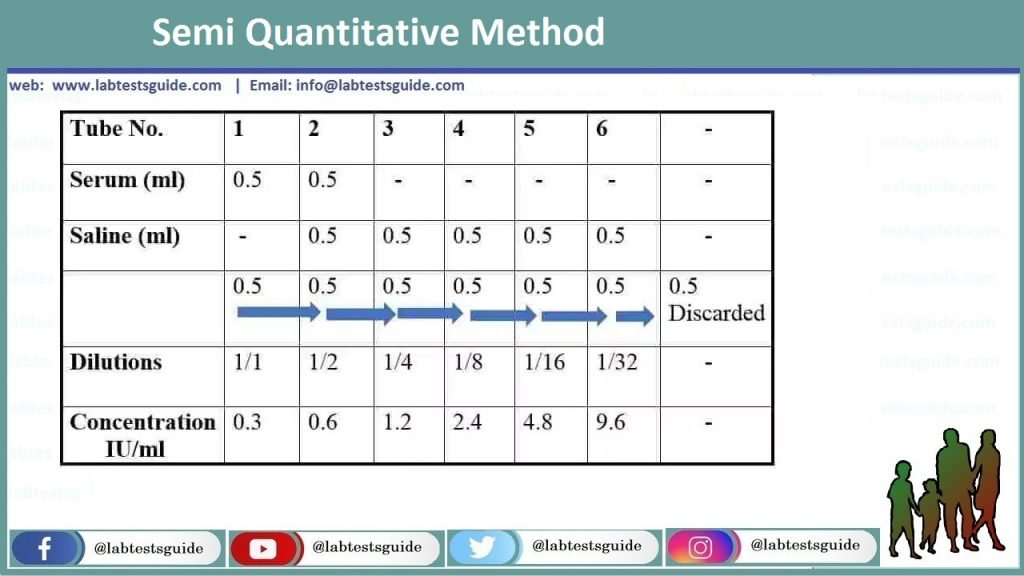Notice that each dilution is three-fold relative to the previous one.In four dilutions, we have covered a range of 181/3 = 60-fold.If that isn't enough range, consider a series of five-fold dilutions:

Parallel Dilution Formula

1/5, 1/25, 1/125, 1/625

Here we've covered a (625/5) = 125-fold range.No matter where the half-max falls in a series of 5-fold dilutions,it is no more than2.2-fold ('middle' [square root] of a 5-fold step) awayfrom a data point -- so the coverage of the range is thorough and even.

When you need to cover several factors of ten (several 'orders of magnitude') witha series of dilutions, it usually makes the most sense to plot the dilutions(relative concentrations) on a logarithmic scale. This avoids bunching mostof the points up at one end and having just the last point way fardown the scale.

Before making serial dilutions, you need to make rough estimatesof the concentrationsin your unknowns, and your uncertainty in those estimates. For example,if A₂₈₀ says you have 7.0 mg total protein/ml, and you thinkthe protein could be anywhere between 10% and 100% pure, then yourassay needs to be able to see anything between 0.7 and 7 mg/ml.That means you need to cover a ten-fold range of dilutions, or maybe a bitmore to be sure.

If the half-max of your assay occurs atabout 0.5mg/ml,then your minimum dilution fold is(700mg/ml)/(0.5mg/ml) = 1,400.Your maximum is(7000mg/ml)/(0.5mg/ml) = 14,000.So to be safe, you might want to cover 1,000 through 20,000.

In general, before designing a dilution series, you need to decide:

1. What are the lowest and highest concentrations (or dilutions)you need to test in order to be certain of finding the half-max? Thesedetermine the range of the dilution series.
2. How many tests do you want to make? This determines the size of theexperiment, and how much of your reagents you consume. More tests will coverthe range in more detail, but may take too long to perform (or cost too much).Fewer tests are easier to do, but may not cover the range in enough detailto get an accurate result.
3. What volume of each dilution do you need to make in order to haveenough for the replicate tests you plan to do?

Now suppose you decide that six tests will be adequate (perhapseach in quadruplicate).Well, starting at 1/1,000, you need five equal dilution steps (giving yousix total dilutions counting the starting 1/1,000) that end ina 20-fold higher dilution (giving 1/20,000). You can decide on a goodstep size easily by trial and error. Would 2-fold work? 1/2, 1/4, 1/8, 1/16, 1/32. Yes, in factthat covers 32-fold, more than the 20-fold range we need. (The exact answeris the 5th root of 20, which your calculator will tell you is 1.82 foldper step. It is much easier to go with 2-fold dilutions and gives about thesame result.)

So, you need to make a 1/1,000 dilution to start with. Then you need toserially dilute that 2-fold per step in five steps. You could make 1/1,000 byadding 1 microliter of sample to 0.999 ml diluent. Why is that a poor choice?Because you can't measure 1 microliter (or even 10 microliters) accuratelywith ordinary pipeters. So, make three serial 1/10 dilutions(0.1 ml [100 microliters] into 0.9 ml): 1/10 x 1/10 x 1/10 = 1/1,000.

Serial Vs Parallel Dilution Method Definition

Now you could add 1.0 ml of the starting 1/1,000 dilution to1.0 ml of diluent, making a 2-fold dilution (giving 1/2,000).Then remove 1.0 ml from that dilution (leaving 1.0 ml for yourtests), and add it to 1.0 ml of diluent in the next tube (giving1/4,000). And so forth for 3 more serial dilution steps (giving1/8,000, 1/16,000, and 1/32,000). You end up with 1.0 ml of each dilution.If that is enough to perform all of your tests, this dilution planwill work. If you need larger volumes, increase the volumes you useto make your dilutions (e.g. 2.0 ml + 2.0 ml in each step).